PARCIAL 2

ASIGNATURA: CÁLCULO

Propósito Asignatura:

Que el estudiante relacione conocimientos de diversas disciplinas (sistemas y reglas o principios medulares) para estructurar ideas, argumentos y crear modelos que den solución a problemas surgidos de la actividad humana, tales como: la distribución inequitativa de los recursos económicos y la propagación rápida de enfermedades, entre otros; así como de fenómenos naturales (cambio climático, contaminación por emisión de gases, etc.), aplicando el razonamiento, el análisis e interpretación de procesos infinitos que involucren razones de cambio.
Que el estudiante analice e interprete las relaciones entre las variables de problemas de la vida cotidiana relacionados con áreas, volúmenes, etc., que impliquen variaciones en procesos infinitos y los resuelva aplicando el teorema fundamental del cálculo.

Relación del Cálculo con otras materias:

Lectura, Expresión Oral y Escrita
Comprensión y escritura de textos, comunicación y argumentación de ideas o soluciones de situaciones problemáticas.
Química y  Bioquímica
Construcción de modelos matemáticos y en la solución de los modelos que resulten de estas formulaciones, graficación de átomos y moléculas en el plano o en el espacio.
Inglés
Traducción y comprensión de textos en una segunda lengua que se requieran utilizar en la solución de problemas matemáticos de la vida cotidiana.
CTSyV
Construcción de modelos matemáticos que representen el desarrollo sustentable, deterioros y/o hechos sociales. TIC Empleo de herramientas computacionales para facilitar el aprendizaje de las Matemáticas. Biología y Ecología Aplicar modelos matemáticos para interpretar procesos biológicos y ecológicos.
Física
Uso de modelos matemáticos, representación gráfica de los fenómenos naturales, conversiones de unidades, etc.
Temas de Administración e Introducción a la Economía Construcción de modelos matemáticos que representen hechos administrativos y económicos.
Dibujo Técnico
Graficación de figuras geométricas, líneas, acotaciones, ángulos, etc.

Competencias propuestas para desarrollar en el estudiante para la materia de Cálculo:

1. Construye e interpreta modelos matemáticos mediante la aplicación de procedimientos aritméticos, algebraicos, geométricos y variacionales, para la comprensión y análisis de situaciones reales, hipotéticas o formales.
2. Formula y resuelve problemas matemáticos, aplicando diferentes enfoques.
3. Explica  e interpreta los resultados obtenidos mediante procedimientos matemáticos y los contrasta con modelos establecidos o situaciones reales.
4. Argumenta la solución obtenida de un problema, con métodos numéricos, gráficos, analíticos o variacionales, mediante el lenguaje verbal, matemático y el uso de las tecnologías de la información y la comunicación.
5. Analiza las relaciones entre dos o más variables de un proceso social o natural para determinar o estimar su comportamiento.
6. Cuantifica, representa y contrasta experimental o matemáticamente las magnitudes del espacio y las propiedades físicas de los objetos que lo rodean.
7. Elige un enfoque determinista o uno aleatorio para el estudio de un proceso o fenómeno, y argumenta su pertinencia.
8. Interpreta tablas, gráficas, mapas, diagramas y textos con símbolos matemáticos y científicos.

Estructura conceptual de la materia de Cálculo:

Historia del Cálculo

SIGLO XVII

***En sus comienzos el cálculo fue desarrollado para estudiar cuatro problemas científicos y matemáticos.

***Newton y Leibniz son considerados los inventores del cálculo pero representan un eslabón en una larga cadena iniciada muchos siglos antes.

***Los trabajos de Newton están motivados por sus propias investigaciones físicas (de allí que tratara a las variables como "cantidades que fluyen")

***Leibniz conserva un carácter más geométrico y, diferenciándose de su colega, trata a la derivada como un cociente incremental, y no como una velocidad.

***Se desata una larga y lamentable polémica a raíz de la prioridad en el descubrimiento del Cálculo.

***La difusión de las nuevas ideas fue muy lenta y al principio sus aplicaciones escasas.

SIGLO XVIII

***Durante buena parte del siglo los discípulos de Newton y Leibniz se basaron en sus trabajos para resolver diversos problemas de física, astronomía e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro de las matemáticas.

***Los hermanos Bernoulli inventaron el cálculo de variaciones.

***Lagrange, también francés, dio un tratamiento completamente analítico de la mecánica, realizó contribuciones al estudio de las ecuaciones diferenciales y la teoría de números, y desarrolló la teoría de grupos.

***El gran matemático del siglo fue el suizo Euler, quien aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y sus aplicaciones. Escribió textos sobre cálculo, mecánica y álgebra que se convirtieron en modelos a seguir para otros autores interesados en estas disciplinas.

SIGLO XIX

***Un problema importante fue definir el significado de la palabra función.

***En 1821, un matemático francés, Cauchy, consiguió un enfoque lógico y apropiado del cálculo y se dedicó a dar una definición precisa de "función continua".

***Gauss, uno de los más importantes matemáticos de la historia, dio una explicación adecuada del concepto de número complejo; estos números formaron un nuevo y completo campo del análisis, desarrollado en los trabajos de Cauchy, Weierstrass y el matemático alemán Riemann.

***Los fundamentos de la matemática fueron completamente transformados durante el siglo XIX, sobre todo por el matemático inglés Boole en su libro Investigación sobre las leyes del pensamiento (1854).

SIGLO XX

***Es importante el aporte realizado por Lebesgue referido a la integración y a la teoría de la medida y las modificaciones y generalizaciones realizadas por matemáticos que lo sucedieron.

***En la Conferencia Internacional de Matemáticos que tuvo lugar en París en 1900, el matemático alemán David Hilbert, quien contribuyó de forma sustancial en casi todas las ramas de la matemática retomó veintitrés problemas matemáticos que él creía podrían ser las metas de la investigación matemática del siglo que recién comenzaba.

***El avance originado por la invención del ordenador o computadora digital programable dio un gran impulso a ciertas ramas de la matemática, como el análisis numérico y las matemáticas finitas, y generó nuevas áreas de investigación matemática como el estudio de los algoritmos. Se convirtió en una poderosa herramienta en campos tan diversos como la teoría de números, las ecuaciones diferenciales y el álgebra abstracta. 

***El conocimiento matemático del mundo moderno está avanzando más rápido que nunca. Teorías que eran completamente distintas se han reunido para formar teorías más completas y abstractas.

***Aunque la mayoría de los problemas más importantes han sido resueltos, otros siguen sin solución. Al mismo tiempo aparecen nuevos y estimulantes problemas y aún la matemática más abstractas encuentra aplicación.

PROGRAMA PARA LA ASIGNATURA DE CÁLCULO.

*Pre-cálculo

• Numeros Reales
• Intervalos
• Desigualdades

*Funciones

• Dominio y contradominio
• Clasificación
• Comportamiento

*Limites

• Limite de una función
• Propiedades
• Continuidad de una función

*Derivada

• Razón de cambio promedio de interpretación geométrica
• Derivación de funciones
• Derivada sucesivas
• Comportamiento

*Integral

• Integral definida
• Integral indefinida

1.-Pre-cálculo

Números Reales

En matemáticas, el conjunto de los números reales (denotado por ℝ) incluye tanto a los números racionales (positivos, negativos y el cero) como a los números irracionales; y en otro enfoque, trascendentes y algebraicos. Los irracionales y los trascendentes (1970) no se pueden expresar mediante una fracción de dos enteros con denominador no nulo; tienen infinitas cifras decimales aperiódicas, tales como: √5, π, el número real log2, cuya trascendencia fue enunciada por Euler en el siglo XVIII.

Los números reales pueden ser descritos y construidos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.

Intervalos

Se llama intervalo al conjunto de números reales comprendidos entre otros dos dados: a y b que se llamanextremos del intervalo.

Intervalo abierto

Intervalo abierto, (a, b), es el conjunto de todos los números reales mayores que a y menores que b.

Intervalo cerrado

Intervalo cerrado, [a, b], es el conjunto de todos los números reales mayores o iguales 
que a y menores o iguales que b.

Intervalo semiabierto por la izquierda

Intervalo semiabierto por la izquierda, (a, b], es el conjunto de todos los números reales mayores que a y menores o iguales que b.

Desigualdades

Igualdades

Cuando dos objetos son iguales si (y solo si) son el mismo objeto. Por ejemplo, la frase "la suma de dos y dos" y la expresión "el cuatro" se refieren al mismo objeto matemático, un cierto número natural. La expresión "es igual a" o "es lo mismo que" se suele representar en matemáticas con el signo ' = ' .

Un enunciado en el que dos expresiones (iguales o distintas) denotan el mismo objeto se llama una ecuación o una igualdad. Un ejemplo de ecuación sería "dos más dos es lo mismo que cuatro", que se suele escribir así:

2   +   2   =   4

Una relación de equivalencia entre los elementos de un conjunto divide el conjunto en una serie de clases. El conjunto de las clases de equivalencia se llama 'conjunto cociente'. Decimos que dos elementos del conjunto original son ' equivalentes ' si pertenecen a la misma clase.

Las igualdades pueden ser:

1) Condicionales, en cuyo caso se cumplen para solo algunos valores de la variable, por ejemplo, si  3x = 6, solo se cumple la igualdad sí   x = 2.

2) Identidades se cumplen para todos los valores permisibles de la variable, por ejemplo: (x – 4) = x – 8x + 16 es una identidad algebraica que se cumple para todos los valores de x.

Desigualdades 

Una desigualdad es una relación que existe entre dos cantidades o expresiones y, que nos indica que tienen diferente valor. Es decir, lo contrario a lo que ocurre en una igualdad. 

En la desigualdad, los términos están relacionados por un símbolo de "mayor que" (>) o "menor que" (<). También existen otros derivados de estos dos. Si alguno de estos dos símbolos aparece acompañado por una línea horizontal por debajo, significa "mayor o igual que" o "menor o igual que", respectivamente. Un ejemplo de una desigualdad es: 2x + 7 < 19 Que se lee como "2 x más 7 es menor que 19". Y representa al conjunto de números para el que esta expresión es verdadera.

2.-Funciones

Conjunto de pares ordenados (x,y) en los que no existen dos pares ordenados con el mismo primer número (es decir, con el mismo valor de “x” y diferente valor “y”).

Dominio de una función

Conjunto de todos los valores admisibles de la variable independiente, es decir, la variable “x”.

Contradominio de una función

El conjunto de todos los valores resultantes de la variable dependiente “y”. Otros nombres para éste son: recorrido (poco empleado en cálculo); ámbito (termino muy reciente para este concepto); imagen (muy utilizado en álgebra y teoría de conjuntos); y rango (muy empleado en cálculo).

CLASIFICACION DE FUNCIONES

Funciones algebraicas

En las funciones algebraicas las operaciones que hay que efectuar con la variable independiente son: la adición, sustracción, multiplicación, división, potenciación y radicación.

Las funciones algebraicas pueden ser:

Funciones explícitas

En las funciones explícitas se pueden obtener las imágenes de x por simple sustitución.

f(x) = 5x - 2

Funciones implícitas

En las funciones implícitas no se pueden obtener las imágenes de x por simple sustitución, sino que es preciso efectuar operaciones.

5x - y - 2 = 0

Funciones polinómicas

Las funciones polinómicas vienen definidas por un polinomio.

f(x) = a0 + a1 x + a1 x² + a1 x³ +··· + an xn

Su dominio es, es decir, cualquier número real tiene imagen.

Funciones constantes

El criterio viene dado por un número real.

f(x)= k

La gráfica es una recta horizontal paralela a al eje de abscisas.

Funciones polinómica de primer grado

f(x) = mx +n

Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.

COMPORTAMIENTO DE FUNCIONES

El comportamiento de las funciones se evidencia mediante la gráfica que describen. A continuación se presentan los cuatro casos de comportamiento de las funciones:

                                          

3.-LIMITES

LIMITE DE UNA FUNCIÓN

El límite de una función de variable real es un concepto fundamental del análisis matemático aplicado a las funciones.

Intuitivamente, el hecho que una función f alcance un límite L en el punto c, significa que el valor de f puede ser tan cercano a L como se desee, tomando puntos suficientemente próximos a c, sin importar el valor que pudiera adquirir f en el punto c.

Aunque implícita en el desarrollo del Cálculo de los siglos XVII y XVIII, la notación moderna del límite de una función se remonta a Bolzano quien, en 1817, introdujo las bases de la técnica épsilon-delta.¹ Sin embargo, su trabajo no fue conocido mientras él estuvo vivo. Cauchy expuso límites en su Cours d'analyse (1821) y parece haber expresado la esencia de la idea, pero no de una manera sistemática.² La primera presentación rigurosa de la técnica hecha pública fue dada por Weierstrass en los 1850 y 1860³ y desde entonces se ha convertido en el método estándar para trabajar con límites.

La notación de escritura usando la abreviatura lim con la flecha debajo es debida a Hardy en su libro A Course of Pure Mathematics en 1908.

PROPIEDADES DE UNA FUNCIÓN

Propiedades generales

Si f(x) y g(x) son funciones de variable real y k es un escala , entonces, se cumplen las siguientes propiedades:

CONTINUIDAD DE UNA FUNCIÓN

En matemáticas, una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función; aunque en rigor, en un espacio métrico como en variable real, significa lo contrario, que pequeñas variaciones de la función implican que deben estar cercanos los puntos. Si la función no es continua, se dice que es discontinua. Una función continua de  en  es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel (más formalmente su grafo es un conjunto conexo).

La continuidad de funciones es uno de los conceptos principales del análisis matemático y de la topología. El artículo describe principalmente la continuidad de funciones real desde una variable real.

4.- DERIVADA

En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

Razón de cambio  promedio de interpretación geométrica

La razón de cambio también conocida como taza de cambio, de variación o de transferencia de la función en el intervalo [a, a+h], que se representa por Δy, es la diferencia entre las ordenadas correspondientes a los puntos de abscisas a y a+h. Es decir, la medida en que una variable cambia con respecto a otra, como por ejemplo la velocidad, la cual es una razón de cambio del espacio con respecto al tiempo: lim(Dx/Dt, t tiende a cero).
RAZÓN DE CAMBIO PROMEDIO es el cociente de las diferencias de f durante el intervalo [a, b]. A la diferencia en las coordenadas x de los puntos de la gráfica de una función f se le llama incremento de x, se le denota mediante Δx que es igual a x2 – x1 es decir, Δx = x2 – x1 asimismo, Δy = y2 – y1 al formar el consiente de cambio en y con los cambios en x podemos escribir:
Δy/Δx donde a este cociente llamamos razón de cambio promedio.Es decir,   Δf(x)/Δx=[f(x+Δx)-f(x)]/ Δx |

Como su nombre lo dice, la razón de cambio promedio da una medición de cuanto cambia la función f cuando x cambia una cantidad “delta x”.

Derivada de una Función

Considerando la función f definida en el intervalo abierto I y un punto a fijo en I, se tiene que la derivada de la función f en el punto  se define como sigue:

,

si este límite existe, de lo contrario, la derivada, no está definida. Esta última expresión coincide con la velocidad instantánea del movimiento continuo uniforme acelerado en cinemática.

Aunque podrían calcularse todas las derivadas empleando la definición de derivada como un límite, existen reglas bien establecidas, conocidas como teoremas para el cálculo de derivadas, las cuales permiten calcular la derivada de muchas funciones de acuerdo a su forma sin tener que calcular forzosamente el límite. Tales reglas son consecuencia directa de la definición de derivada y de reglas previas, como puede apreciarse en todo buen texto de cálculo infinitesimal.

También puede definirse alternativamente la derivada de una función en cualquier punto de su dominio de la siguiente manera:

La cual representa un acercamiento de la pendiente de la secante a la pendiente de la tangente ya sea por la derecha o por la izquierda según el signo de . El aspecto de este límite está relacionado más con la velocidad instantánea del movimiento uniformemente acelerado que con la pendiente de la recta tangente a una curva.

No obstante su aparente diferencia, el cálculo de la derivada por definición con cualquiera de los límites anteriormente expresados, proporciona siempre el mismo resultado.

INTEGRAL DEFINIDA

La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos sumandos, infinitamente pequeños.

El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación, es muy común en la ingeniería y en la ciencia también; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.

Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.

INTEGRAL INDEFINIDA

En cálculo infinitesimal, la función primitiva o antiderivada de una función f es una función F cuya derivada es f, es decir, F ′ = f.

Una condición suficiente para que una función f admita primitivas sobre un intervalo es que sea continua en dicho intervalo.

Si una función f admite una primitiva sobre un intervalo, admite una infinidad, que difieren entre sí en una constante: si F₁ y F₂ son dos primitivas de f, entonces existe un número real C, tal que F₁ = F₂ + C. A C se le conoce como constante de integración. Como consecuencia, si F es una primitiva de una función f, el conjunto de sus primitivas es F + C. A dicho conjunto se le llama integral indefinida de f y se representa com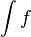o:

                                                               ó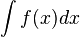   

El proceso de hallar la primitiva de una función se conoce como integración indefinida y es por tanto el inverso de la derivación. Las integrales indefinidas están relacionadas con las integrales definidas a través del teorema fundamental del cálculo, y proporcionan un método sencillo de calcular integrales definidas de numerosas funciones.

Autoevaluación

A.-Números Reales. Elige la respuesta correcta.

1.       ¿Qué tipo de números incluyen tanto a los números irracionales como a los racionales?

a)Reales

b)Irreales

c)Imaginarios

d)Naturales

2.       ¿Qué tipo de números nos sirven para contar?

a)Complejos

b)Contadores

c)Naturales

d)Irracionales

3.       (…) es un número imaginario.

a)1

b)Raiz de -3

c)Raiz de 25

d)-50

4.       Las constantes p y e pertenecen al conjunto de números llamado…

a)Racionales

b)Enteros

c)Naturales

d)Irracionales

5.       Los números reales son todos aquellos números que se pueden ubicar en…

a)Plano Cartesiano

b)Recta Numérica

c)Grafica

d)Diagrama de Arbol

B.-Funciones. Elige la respuesta correcta.

6.       Es un objeto matemático que se utiliza para expresar la dependencia entre dos magnitudes.

a)Función

b)Grafica

c)Recta Numérica

d)Potencia

7.       Forma de representar la información proporcionada por una función.

a)Plano cartesiano

b)Recta Numérica

c)Grafica

d)Línea de tendencia

8.       ¿Qué clasificación de funciones incluye a las funciones Trigonométricas?

a)Trascendentales

b)Algebraicas

c)Explicitas

d)Implicitas

9.       Cuando dos distintas funciones dependen una de la otra se les llama…

a)Lineales

b)Exponenciales

c)Compuestas

d)Directas

10.   ¿De qué se compone una función?

a)Dominio y Contradominio

b)Grafica y Ecuacion

c)Dominio y  Ecuacion

d)Contradominio y Grafica

 Respuestas

1.a 2.c 3.b 4.d 5.b 6.a 7.c 8.a 9.c 10.a